Universal Approximation

The universal approximation is the ability of a certain set of mathematical functions or models to mimic or simulate any other function with precision, yielding a proportionate degree of complexity when needed. It can be well thought of in the arena of machine learning and artificial intelligence

Introduction:

Case of neural networks, the universal approximation theorem was first proved by George Cybenko and the theorem states that a feedforward neural network with one hidden layer having a finite number of neurons is capable of approximating any continuous function of compactness of real numbers under conditions. Simultaneously, Horbik improved this theorem of multi-layer neural networks.

Importance:

Universal approximation has a huge application in various fields, including sensitive ones:

1) Functions: Neural networks can be used to approximate complex functions such as those in math, physics, finance, and engineering which are difficult to model.
2) Pattern recognition: For image processing, spoken language recognition, and natural language processing; neural networks are similar to the human brain and can approximate complex patterns to extract information contained in unstructured data.
3) Control Systems: Neural networks approximate nonlinear systems that are used to design and implement different control and optimization systems due to their ability to handle time-dependent data.
4) Prediction & Forecasting: Using the artificial neural networks we can approximate the relationships of the nonlinear time series data which can give us a more accurate picture of the banking and stock markets as well as for the weather.

Explanation and Summary:

The universal approximation power of neural networks is presented by their ability to approximate any complex function. Therefore, it is one of the most usable tools and can be used in solving a wide field of black-box problems in various areas. The key to doing so is to take advantage of the capability of the artificial neural networks to mimic the neural activity of the human brain, and thus be able to create advanced models, which can represent any complex system and learn from the data being processed in them. Nevertheless, it is of great signification to specify that while the universal approximation (theory) supports the development of the guarantees, its implementation and training should be thoroughly thought out with consideration of various aspects, such as data quality, model architecture, and optimization techniques to gain the targeted performance.

Theorem

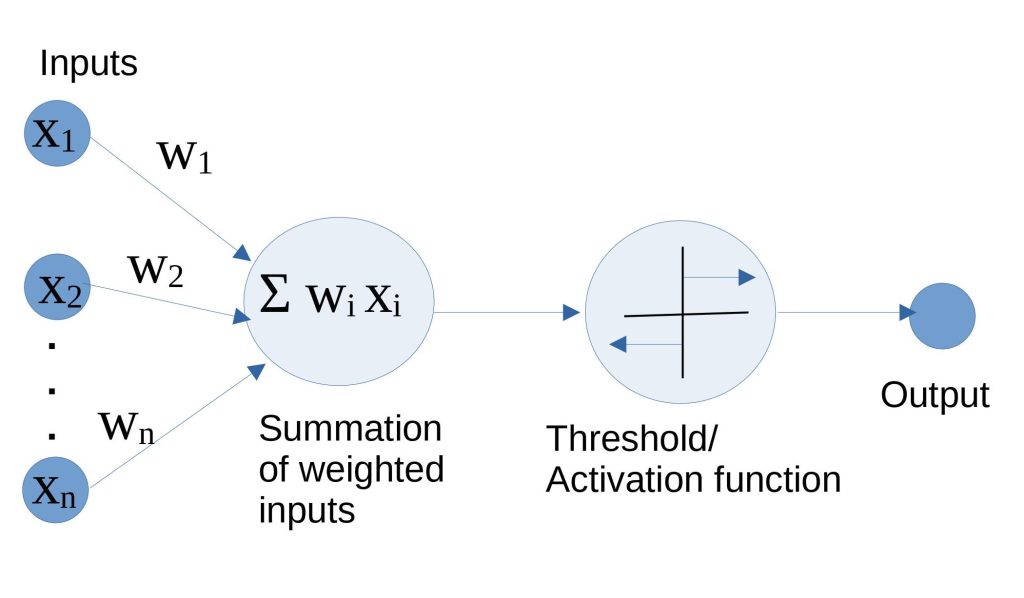
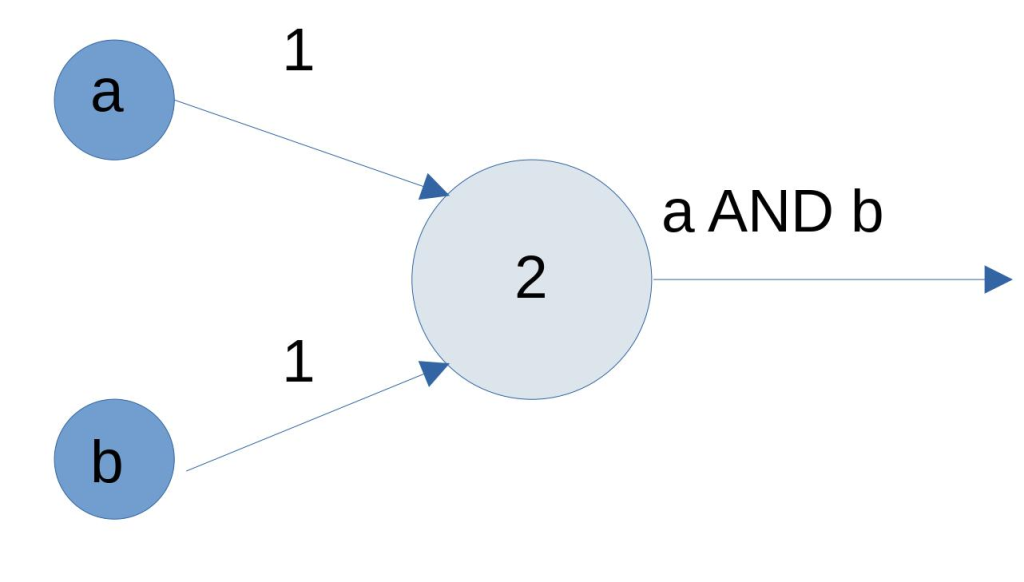
Perceptrons: Perceptrons are the elemental processing devices, which are embedded in the neural networks. These units do computing by multiplying inputs with respective weights and afterward getting the sum. The sum is put through an activation function such as the sigmoid function, which gives the read or not-read signal, in this case, based on a certain threshold level. Without activation functions the neural networks would become just convolutional and add some weights concerning inputs stressing the fact that in contrast to linear effects, non-linearity is also important.

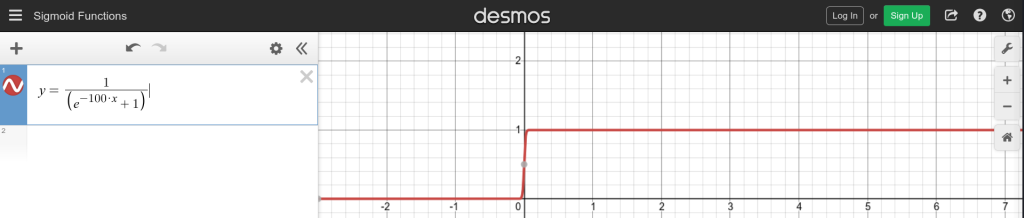
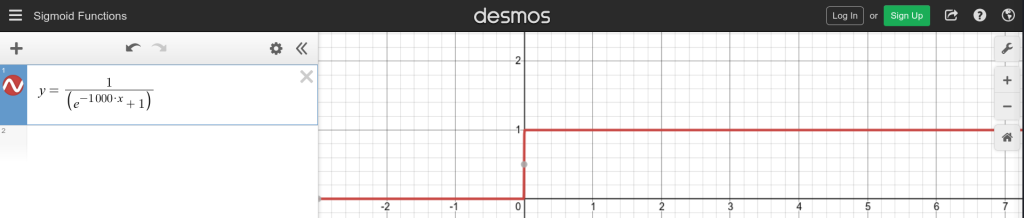
Converting Sigmoid to Step Function: The process of converting the sigmoid function, where the output is the real number between 0 and 1, to give a step function that produces the output of binary form (0 or 1). Such conversion is driven by the objective of reducing the complexity of the calculations, specifically during processing outputs from different network layers. As required, it can be adjusted precisely for a step function where setting slightly modified patterns is instrumental in easy manipulations in the organization of neural networks. With a weight of 1000 chosen as optimal, and with adjustments to bias if necessary, the sigmoid function effectively emulates a step function, facilitating easier threshold-based computations in subsequent neural network analyses.

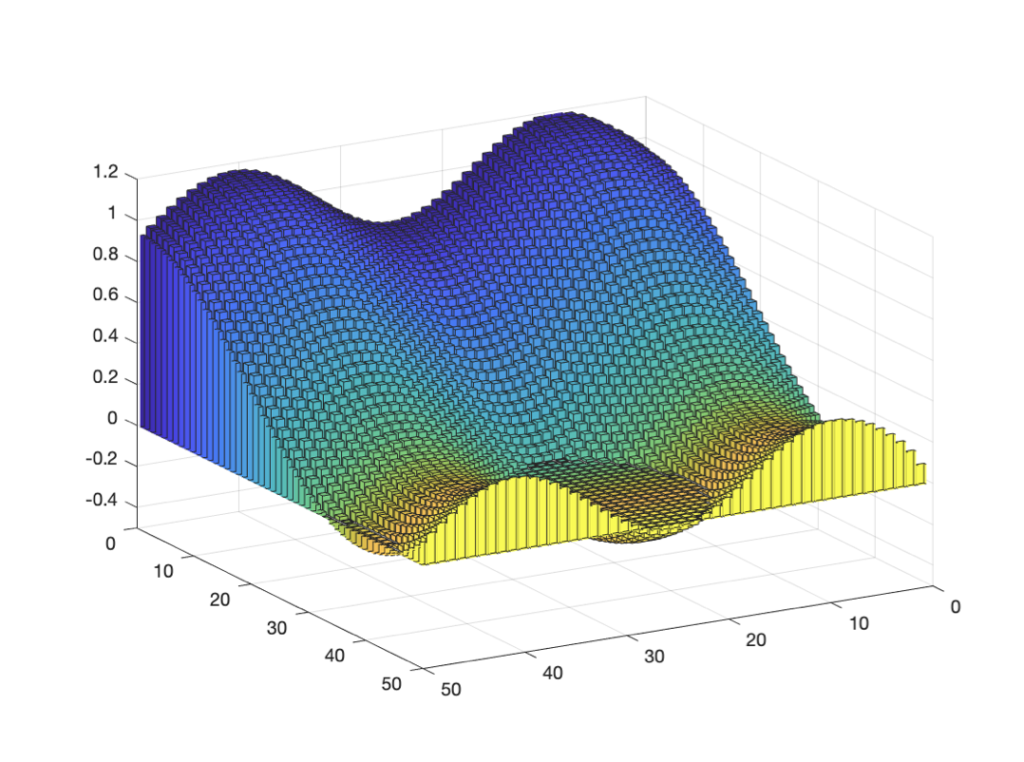
Experimentation with Perceptrons: Altering with different iterations of perceptrons, demonstrates how neural networks can be made actionable. Functions like Boolean and or threshold activation done through the use of perceptrons are being presented using plotting to support how these units effectively embody very simple computational tasks. This kind of communal work enables to discovery of the abilities of neural networks at the basic level and thus it creates an excellent basis for more complex options.

Universal Approximation Demo

Purpose of this demo

The demo integrates the basis of universal approximation, which postulates that a single-layer neural network can be used to achieve any high degree of precision if the model has the same number of hidden neurones as the continuous function.

1. Neural Network Architecture: The key element of the demo is a simple neural network architecture with one hidden layer. The change in the extent of nodes in that hidden layer reveals how the neural networks run more like precision operations with heavier hidden layers and approximate complex functions more precisely.
2. Function Approximation: Switch to making such predictions for both functions, being either sine or cosine or other functions. The Neural Networks here then represent this by changing the biases and the weights during the training.
3. Interactivity: Demonstrations have an interactive interface that includes the capability to adjust the number of layers in the hidden layer and target function. This makes it possible for users to conduct their simulation using different setups to see how well the neural network models and their approximation.
4. Real-Time Visualisation: The gradual changes in the demo target function approximation made by the neural network are visualized in real-time as the demo user interactively selects relevant input and output parameters. Such visualization helps humans locate how a neural network gradually gets used to an approximate method of complex functions by making an iterative adjustment to its parameters.

This demo is a practical depiction of the universal approximation, where the users can understand under which neural networks approach different functions in a way that reinforces their understanding of the concept and concretises the same theory.

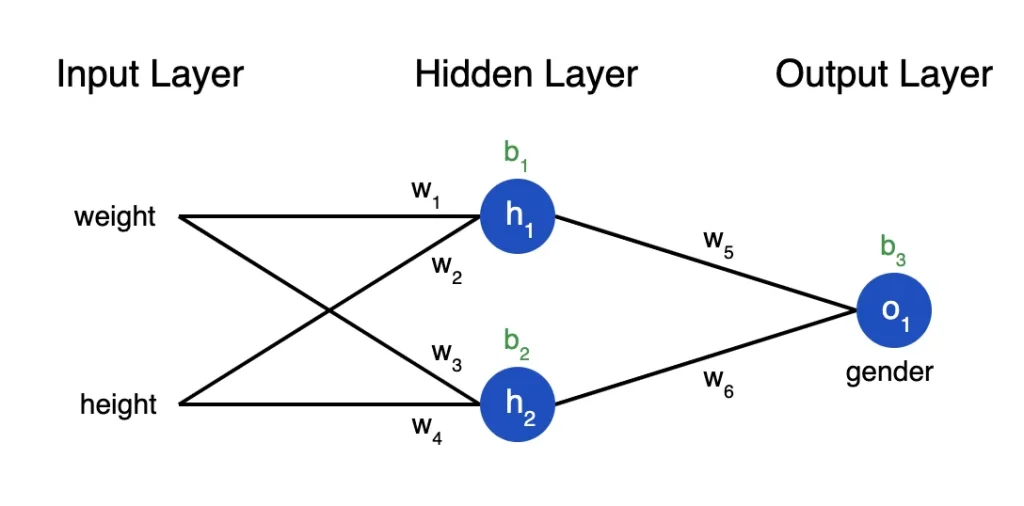
Why are there neurones in the hidden layers?

Neural network neurons that belong to the hidden layers are responsible for approximating functions that are complex. Every neuron in the hidden layer has its part in the network's capacity to transform and represent information from the input data in different ways and patterns.

Why neurone in hidden layers are necessary?

1. Feature Representation: The hidden layers will be responsible for discovering important patterns in the input data and the way to facilitate this process will be through the use of deep learning. Neurons in the hidden layer are processing inputs that are a given portion of the features and it is the job of these neurons to learn how to detect relationships and patterns.
2. Non-linear Mapping: While the linear activation function used in the hidden layers may be the most useful one, it is the non-linear activation functions used in the hidden layers such as the sigmoid, tanh, or ReLU function that are responsible for introducing non-linearity to the network. This results in a neural network that can, approximate complex, non-linear functions which was not possible to do under the simple linear model.
3. Ranked Representation: The models with multiple hidden layers make it possible for "deep" neural networks to learn this type of pattern or structure from the data. On the character level, each layer improves the representation of the input data's features being more sophisticated in their abstraction allowing the net to comprehend complex interrelations on various levels of generalisation.
4. Expressiveness: The expressiveness or capacity of the number of neurons in the intermediate layers determines the number of neurons in the hidden layers. Neurons largely increase the capacity of the network to gain more functions and patterns of the data. On the other hand, the great number of neurons may overfit the results, and further fewer neurons will generate underfitting results, so both are not desirable.
5. Generalisation: Establishing new layers during the process of learning the nets with hidden layers allows it to fit the well to not only seen but also unseen data. By training the network to model the original function by learning from training data, which is later used to make precise predictions or classifications on new, unseen cases (samples).

As a result, the outcome neurones highly influence how the neural network approximates complex functions, how they can figure out the meaningful inputs from these, and how good generalization is applied to new examples. finding the number of neurons in the hidden layers is one key parameter of the neural network, and it is a critical implication for the construction of high-performance networks for specific tasks.

Links and references

Upadhyay, K. (2021) 'Beginner’s Guide to Universal Approximation Theorem', Analytics Vidhya. Available at: https://www.analyticsvidhya.com/blog/2021/06/beginners-guide-to-universal-approximation-theorem/ (Accessed: March 15, 2024)

Nielsen, M. (2019) 'CHAPTER 4: A visual proof that neural nets can compute any function', neuralnetworksanddeeplearning.com. Available at: http://neuralnetworksanddeeplearning.com/chap4.html (Accessed: March 15, 2024)

Lörke, A., Schneider, F., Heck, J., & Nitter, P. (2019) 'Cybenko’s Theorem and the capability of a neural network as function approximator', University of Wuerzburg. Available at: https://www.mathematik.uni-wuerzburg.de/fileadmin/10040900/2019/Seminar__Artificial_Neural_Network__24_9__.pdf (Accessed: March 15, 2024)

Abiodun, O. I., Jantan, A., Omolara, A. E., Dada, K. V., Mohamed, N. A., & Arshad, H. (2018) 'State-of-the-art in artificial neural network applications: A survey', Heliyon, 4(11), e00938. Available at: https://doi.org/10.1016/j.heliyon.2018.e00938 (Accessed: March 15, 2024)

The Harvard style referencing for the provided article would be:

Sahay, M. (2020) 'Neural Networks and the Universal Approximation Theorem: And the boom of deep neural networks in recent times', Towards Data Science. Available at: https://towardsdatascience.com/neural-networks-and-the-universal-approximation-theorem-8a389a33d30a (Accessed: March 15, 2024)

Bhardwaj, A. (2020) 'What is a Perceptron? – Basics of Neural Networks: An overview of the history of perceptrons and how they work', Towards Data Science. Available at: https://towardsdatascience.com/what-is-a-perceptron-basics-of-neural-networks-c4cfea20c590 (Accessed: March 15, 2024).

Tuzsuz, D. (Year unknown) 'Sigmoid Function', LearnDataSci. Available at: https://www.learndatasci.com/glossary/sigmoid-function/ (Accessed: March 15, 2024)

Author unknown (2019) 'Neural Networks: What can a network represent', Deep Learning, Fall 2019. Available at: https://www.cs.cmu.edu/~bhiksha/courses/deeplearning/Fall.2019/www.f19/document/lecture/lecture-2.pdf (Accessed: March 15, 2024)